Mathematics for Physicists

13 Fourier analysis

In Chapter 5 we discussed how functions could be represented as power series using the expansions of Taylor and Maclaurin. Those expansions are valid only within certain radii of convergence, where the functions must be continuous and infinitely differentiable. However, this is not the only way that functions can be expressed as a series. In this chapter we will consider another expansion, which may also be used for functions that are neither continuous nor differentiable at certain points. To start with, the discussion will be centred on functions f(x) that are periodic, that is, they obey the relation f(x) = f(x + np), where p is the period, and n = 1, 2, …. Many functions that occur in physical science are of this type. For example, solutions of the equations for problems concerning wave motion involve sinusoidal functions. The form of f(x) can be arbitrarily complicated, such as the continuous function shown in Figure 13.1. We shall also see that the method can be applied to functions that are only defined in a finite range of x. This leads naturally to an important extension in which non-periodic functionsf(x), defined for all x, can be expressed in terms of simple sinusoidal functions, provided f(x) → 0 rapidly enough as x → ∞. Such expressions, called Fourier transforms, are extremely useful and will be discussed in Section 13.3.

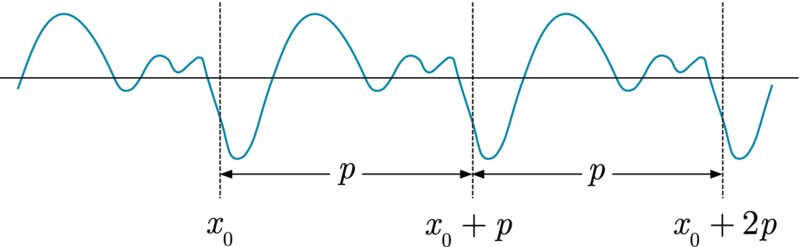
Figure 13.1 An arbitrary ...