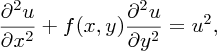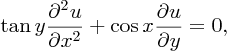Mathematics for Physicists

16 Partial differential equations

In Chapters 14 and 15 we discussed ordinary differential equations and their solutions. These are equations that contain a dependent variable y, which is a function of a single variable x, and derivatives of y with respect to x. In this chapter, we extend the discussion to similar equations that involve functions of two or more variables x₁, x₂, …, x_n. These are called partial differential equations (PDEs) because the functional form analogous to (14.2) in general contains partial differentials with respect to several variables, including mixed derivatives. If we consider a function u of just two variables x₁ = x and x₂ = y, then examples of partial differential equations are

(16.1a)

(16.1b)

and

(16.1c)

where f(x, y) is an arbitrary function of x and y.

By analogy with the definitions in Chapter 14, the degree of the equation is defined as the power to which the highest order derivative is raised after the equation is rationalised, if necessary; and the order of a partial differential equation is the order of the highest derivative in the equation. Thus (16.1a) is first-order and (16.1b) and (16.1c) are second-order equations. In addition, all ...