CHAPTER 8
Lp SPACES
Lp spaces are spaces of functions whose pth power is integrable. For functions in a Lp space, we can define norms and metrics and study the convergence of sequences of functions. In this chapter, we introduce the concepts of Lp spaces and some important inequalities for functions in the Lp spaces.
8.1 Basic Concepts and Facts
Definition 8.1 (Lp Space). Let (S, ∑, μ) be a measure space and p ![]() (0, ∞]. Then Lp(S, ∑, μ) is defined as
(0, ∞]. Then Lp(S, ∑, μ) is defined as
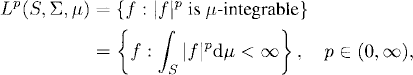
and
![]()
Definition 8.2 (Lp Norm). Let p ![]() (0, ∞] and f
(0, ∞] and f ![]() Lp(S, ∑, μ). The norm of f on LP(S, ∑, μ) is defined as
Lp(S, ∑, μ). The norm of f on LP(S, ∑, μ) is defined as
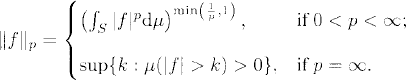
When p = ∞, the norm is called the infinite norm or the maximum norm.
Definition 8.3 (Metric Space). Let S be a set and d : S × S → [0, ∞] be a function. (S, d) is called a metric space if for all x, y, z ![]() S,
S,
Get Measure, Probability, and Mathematical Finance: A Problem-Oriented Approach now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

