Measure, Probability, and Mathematical Finance: A Problem-Oriented Approach

CHAPTER 12

INDEPENDENCE

Independence is an important concept in probability theory. Intuitively, two events are independent if the occurrence of one event does not make the other happen more or less. In this chapter, we will introduce the concept of independence of events and random variables.

12.1 Basic Concepts and Facts

Definition 12.1 (Independent σ-Algebras). Let (Ω, , P) be a probability space. Sub-σ-algebras of are considered independent if and only if

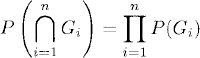
for all sets .

Let , i (an arbitrary index set) be an arbitrary family of sub-σ-algebras of . The are deemed independent if and only ...