CHAPTER 25
MARTINGALE CONVERGENCE THEOREMS
Martingale convergence theorems state that under certain conditions, a martingale, submartingale, or supermartingale converges to a limiting random variable. In this chapter, we shall present several martingale convergence theorems.
25.1 Basic Concepts and Facts
Definition 25.1 (Crossing of Real Numbers). Let {xn : n ≥ 0} be a sequence of real numbers. Let a < b be real numbers. The sequence {τn(a, b) : n ≥ 0} of crossings with respect to the sequence {xn : n ≥ 0} is defined by
(25.1a) ![]()
and for every n ≥ 1, we have
(25.1b) 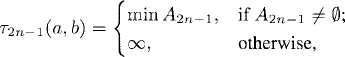
(25.1c) 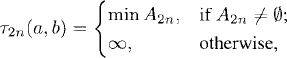
where A2n−1 = {k ≥ τ2n−2 : xk ≤ a} and A2n = {k ≥ τ2n−1 : xk ≥ b}.
Definition 25.2 (Crossing of Random Variables). Let{Xn : n ≥ 0} be a sequence of real random variables. Let a < b be real numbers. The sequence {τn(a, b) : n ≥ 0} of crossings with respect to the sequence {Xn : n ≥ 0} is defined as follows. For every ω ![]() Ω, {τn(a, b)(ω) : n ≥ 0} is the sequence of crossings with respect to the sequence {Xn(ω) : n ≥ 0}.
Ω, {τn(a, b)(ω) : n ≥ 0} is the sequence of crossings with respect to the sequence {Xn(ω) : n ≥ 0}.
Definition 25.3 (∞). Let {n : n ≥ 0} be a filtration. Then ∞ is the σ-algebra generated by :
Theorem ...
Get Measure, Probability, and Mathematical Finance: A Problem-Oriented Approach now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

