CHAPTER 29
MARKOV PROCESSES
A Markov process is a stochastic process that has the Markov property. In other words, a stochastic process is called a Markov process if at every time t, the conditional probability law of the process given the past depends only on the present state. Intuitively, a Markov process is a process that does not have memory. In this chapter, we present the mathematical definition of Markov processes and relevant results.
29.1 Basic Concepts and Facts
Definition 29.1 (Conditional Independence). Let (Ω, 
, P) be a probability space. Let 
be sub-σ-algebras of . Then 
are said to be conditionally independent given 
if
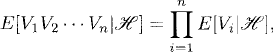
where Vi is an arbitrary positive random variable in m
i, i = 1, 2,…, n. Here mi is the set of all i-measurable functions.
Definition 29.2 (Markov Process). Let ...
Get Measure, Probability, and Mathematical Finance: A Problem-Oriented Approach now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
