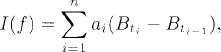Measure, Probability, and Mathematical Finance: A Problem-Oriented Approach

CHAPTER 31

THE WIENER INTEGRAL

The Wiener integral is a simple stochastic integral where the integrand is a deterministic function. In this chapter, we present a definition and some results of the Wiener integral.

31.1 Basic Concepts and Facts

Definition 31.1 (Function Space L²[a, b]). The function space

denotes the space of all real-valued square Lebesgue integrable functions on [a, b], where μ is the Lebesgue measure.

Definition 31.2 (Function Space L²(Ω, , P)). The function space

denotes the space of all square integrable real-valued random variables with inner product X, Y = E(XY).

Definition 31.3 (Wiener Integral of Step Functions). Let f be a step function in L²[a, b] given by

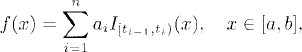
where a = t₀ < t₁ < ··· < t_n = b. The Wiener integral of f is defined as

(31.1)

where {B_t}_t≥0 is the standard ...