Chapter 6
Bootstrap
6.1 Introduction
We begin with an example of the simplest type of bootstrapping in this section, then discuss the idea behind the bootstrap, implementation by random sampling, using the bootstrap to estimate standard error and bias, the central limit theorem and different types of bootstraps, the accuracy of the bootstrap, confidence intervals, hypothesis tests, planning clinical trials, and the number of bootstrap samples needed and ways to reduce this number, and we conclude with references for additional reading.
Figure 1 shows a normal quantile plot of arsenic concentrations from 271 wells in Bangladesh, from http://www.bgs.ac.uk/arsenic/bangladesh/Data/SpecialStudyData.csv referenced from statlib http://lib.stat.cmu.edu/datasets. The sample mean and standard deviation are 
= 124.5 and s = 298, respectively.
Figure 1: Arsenic concentrations in 271 wells in Bangladesh
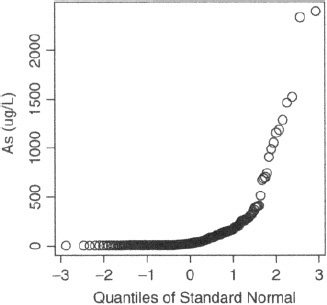
The usual formula standard error is 
= 18.1, and the usual 95% confidence interval 
is (88.8, 160.2). This interval may be suspect because of the skewness of the data, despite the ...
Get Methods and Applications of Statistics in Clinical Trials, Volume 2: Planning, Analysis, and Inferential Methods now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
