Series
4.1 Introduction
4.1.1 Definition
In general a series sn is defined as a sum of a given number of terms ai such that
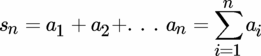
If n = ∞, the series is said to be infinite series. If n is finite, it is said to be a finite series.
4.1.2 Convergence
In most practical applications, a series will have to be evaluated up to a given upper bound n. The higher this bound is chosen, the more exact the solution, but also the more time-consuming, complicated and computationally expensive the solution will become. Therefore a suitable trade-off for n must be found.
However, some of the more important series actually sum up to ...
Get Microfluidics: Modeling, Mechanics and Mathematics now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

