Model Building in Mathematical Programming, 5th Edition

Chapter 3

Building linear programming models

3.1 The importance of linearity

It was pointed out in Section 1.2 that a linear programming model demands that the objective function and constraints involve linear expressions. Nowhere can we have terms such as appearing. For many practical problems, this is a considerable limitation and rules out the use of linear programming. Non-linear expressions can, however, sometimes be converted into a suitable linear form. The reason why linear programming models are given so much attention in comparison with non-linear programming models is that they are much easier to solve. Care should also be taken, however, to make sure that a linear programming model is only fitted to situations where it represents a valid model or justified approximation. It is easy to be influenced by the comparative ease with which linear programming models can be solved compared with non-linear ones.

It is worth giving an indication of why linear programming models can be solved more easily than non-linear ones. In order to do this, we use a two-variable model, as it can be represented geometrically.

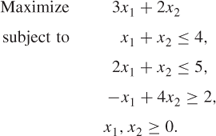
The values of the variables x₁ and x₂ can be regarded as the coordinates of the points in Figure 3.1.

Figure 3.1

The optimal solution is represented by point A where ...