10.5 Annex 5 – Detailed Mathematical Demonstrations
10.5.1 Basic results About Vector Random Variables and Matrices
Recall the following basic vector probabilistic results.
Considering X, as a p-dimensional random vector, and H, a q∗p matrix generating Y (of dimension q), then:
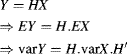
Considering any r∗s matrix denoted as D, then the symmetric matrix DD′ is also semi-positive definite. Indeed, for any vector y of dimension s, then:
![]()
The following property is useful in the context of model identifiability (Chapter 6):
H is a full-rank (i.e. injective) q∗p matrix H′H is an invertible p∗p matrix.
Proof
Suppose H is injective, then:
![]()
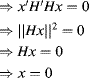
which proves that H′H is also injective. Being a p∗p matrix, it is invertible.
Conversely, if H′H is invertible then:
![]()
which proves that H has a void kernel, that is, it is injective.
This property still holds if H′RH is invertible, R being a definite-positive q∗q matrix. Indeed, R may be decomposed under Cholesky as a product of a q∗q matrix and its transpose:
Get Modelling Under Risk and Uncertainty: An Introduction to Statistical, Phenomenological and Computational Methods now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

