Modern Control System Theory and Design, 2nd Edition

APPENDIX B

PROOF OF THE NYQUISTSTABILITY CRITERION

The Nyquist stability criterion can be derived from Cauchy’s residue theorem, which states that

Let us replace g(s) by f′(s)/f(s), where f(s) is a function of s which is single valued on and within the closed contour C and analytic on C. Observe that the singularities f′(s)/f(s) occur only at the zeros and poles of f(s). The residue may be found at each singularity with multiplicity of the order of zeros and poles taken into account. The residues in the zeros of f(s) are positive and the residues in the poles of f(s) are negative. Therefore, if f(s) is not equal to zero along C, and if there are not at most a finite number of singular points that are all poles within the contour C, then

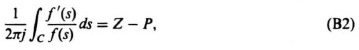
where Z = number of zeros of f(s) within C, with due regrd for their multiplicity of order, and P = number of poles of f(s) within C, with due regard for their multiplicity of order. The left-hand side of Eq. (B2) may be written as

In general, f(s) will have both real and imaginary parts along the contour C. Therefore, its logarithm can be written as

If we assume that f(s) is not zero anywhere on the contour C, the integration of Eq. (B3) results ...