Modern Control System Theory and Design, 2nd Edition

2.20.  REVIEW OF MATRIX ALGEBRA

The classical methods of describing a linear system by means of transfer functions, block diagrams, and signal-flow graphs have thus far been presented in this chapter. An inherent characteristic of this type of representation is that the system dynamics are described by definable input-output relationships. Disadvantages of these techniques, however, are that the initial conditions have been neglected and intermediate variables lost. The method cannot be used for nonlinear, or time-varying systems. Furthermore, working in the frequency domain is not convenient for applying modern optimal control theory, discussed in Chapter 6 of the accompanying volume, which is based on the time domain. The use of digital computers also serves to focus on time-domain methods. Therefore, a different set of tools for describing the system in the time domain is needed and is provided by state-variable methods. As a necessary preliminary, matrix algebra is reviewed in this section [5, 10].

A matrix A is a collection of elements arranged in a rectangular or square array defined by

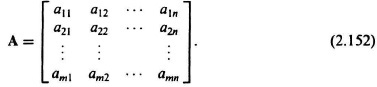
The order of a matrix is defined as the total number of rows and columns of the matrix. For example, a matrix having m rows and n columns is referred to as an m × n matrix. A square matrix is one for which m = n. A column matrix, or vector, is one for which n = 1, and is represented in the ...