Modern Portfolio Theory: Foundations, Analysis, and New Developments, + Website

Chapter 10

Non-Mean-Variance Investment Decisions

The mean-variance investment decision criterion is relevant when asset returns are normally distributed or investors' utility functions are quadratic.¹ In other words, the mean-variance approach holds in the circumstances that the two parameters, mean and variance, are sufficient to describe the investment environment. Therefore, when asset returns are not normally distributed or utility functions are not quadratic, other investment decision tools are needed.² This chapter introduces six other portfolio selection criteria: the geometric mean return (GMR) criterion, the safety-first criterion, value at risk (VaR), semivariance, stochastic dominance, and the mean-variance-skewness criterion. Although some of these criteria still use the first and second moment (mean and variance), they do not require a specific statistical distribution.

10.1 Geometric Mean Return Criterion

The geometric mean of past historical returns, , is defined as

10.1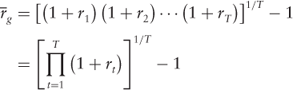

Instead of adding together returns to obtain the mean return, one plus the holding period return is serially multiplied. In historical return observations we assume that each of the observations occurs equally likely, that is, with equal probability of . Alternatively, when the probability of each ...