Nonlinear Image Processing

398 DANIEL L. LAU AND GONZALO R. ARCE

z

9

[--"~g= I/~g= 1/4/g= i/8

.]

2 ..............................................

r.)

~o

<

RADIAL FREQUENCY

4 l g=l/2\ ~ [

g= 1/8"~=.1/4 ~ I'~ ::

0 0.5 0.7071

RADIAL FREQUENCY

(a) h = 0.5

z

9

1

2L_ l g-l,2 .g=i,.6 ]

~0 RADIAL FREQUENCY

4

~ I g=l/4",~ ~'-~ ~

0'- ~-.:--.=--- v ~ v v -----~.- i

0 0.5 0.7071

RADIAL FREQUENCY

(b) h = 1.0

1 ~ 0

~0 RADIAL FREQUENCY

4 ......

/

g=l/8"~ -~r~,_ i

0

0 0.5 0.7071

RADIAL FREQUENCY

(c) h = 1.5

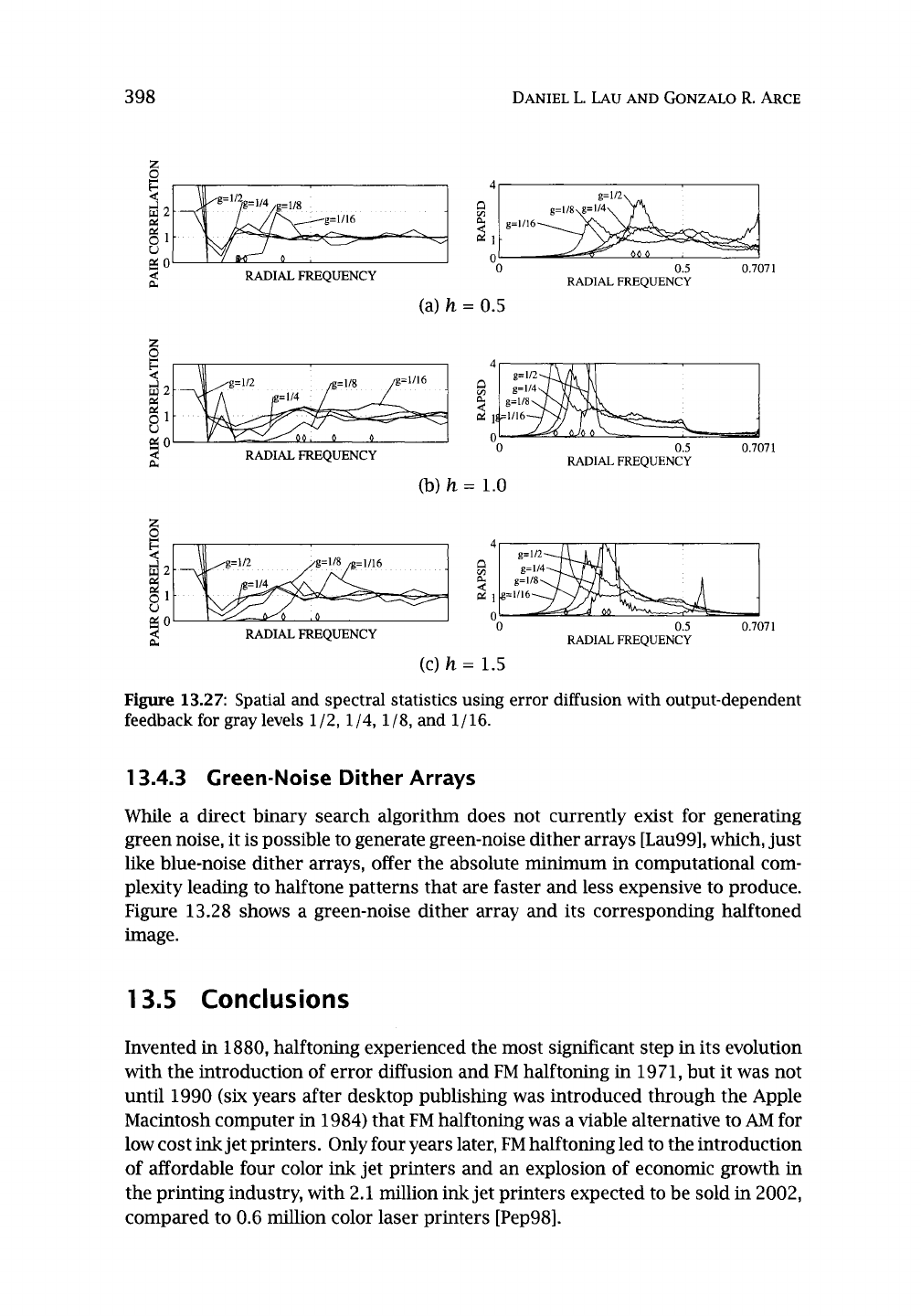
Figure 13.27: Spatial and spectral statistics using error diffusion with output-dependent

feedback for gray levels 1 / 2, 1 / 4, 1 / 8, and 1 / 16.

13.4.3 Green-Noise Dither Arrays

While a direct binary search algorithm does not currently exist for generating

green noise, it is possible to generate green-noise dither arrays [Lau99], which, just

like blue-noise dither arrays, offer the absolute minimum in computational com-

plexity leading to halftone patterns that are faster and less expensive to produce.

Figure 13.28 shows a green-noise dither array and its corresponding halftoned

image.

1 3.5 Conclusions

Invented in 1880, halftoning experienced the most significant step in its evolution

with the introduction of error diffusion and FM halftoning in 1971, but it was not

until 1990 (six years after desktop publishing was introduced through the Apple

Macintosh computer in 1984) that FM halftoning was a viable alternative to AM for

low cost ink jet primers. Only four years later, FM halftoning led to the introduction

of affordable four color ink jet printers and an explosion of economic growth in

the printing industry, with 2.1 million ink jet printers expected to be sold in 2002,

compared to 0.6 million color laser printers [Pep98].

CHAPTER 13: DIGITAL HALFTONING

399

Figure 13.28: (a) Green-noise dither array and (b) resulting halftoned image.

Today, we stand on the verge of a new technological revolution in printing

as printers are achieving ultrahigh resolutions, but to take full advantage of the

smaller dot sizes, a fundamental change must occur in the manner in which

printed dots are arranged. Green noise represents that fundamental change, and

as green noise is extended from theory to practice, the number of algorithms that

generate it will dramatically increase since only a handful currently exist. Issues of

particular importance include computational complexity and color reproduction.

References

[Ami94] I. Amidor, R. D. Hersch, and V. Ostromoukhov. Spectral analysis and mini-

mization of Moir~ patterns in color separation.

J. Electron. Imag.

3(7), 295-317

(July 1994).

[Ana92] M. Analoui and J. P. Allebach. Model based halftoning using direct binary

search. In

Human Vision, Visual Processing, and Digital Display III,

Proc. SPIE

Vol. 1666, pp. 96-108 (August 1992).

[Bar64a] M. S. Bartlett. The spectral analysis of a point process.

J. R. Statist. Soc.

Ser. B

25(2), 264-280 (February 1964).

[Bar64b] M. S. Bartlett. The spectral analysis of two-dimensional point processes.

Biometrika

51(12), 299-311 (December 1964).

[Bla93] D. Blatner and S. Roth.

Real World Scanning and Halftones.

Addison-Wesley,

Berkeley, CA ( 1993).

[Cam96] F.W. Campbell, J. J. Kulikowski, and J. Levinson. The effect of orientation

on the visual resolution of gratings.

J. PhysioL

187(2), 427-436 (November

1996).