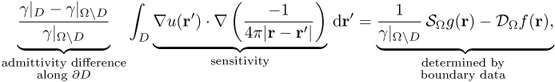Nonlinear Inverse Problems in Imaging

Chapter 8

Anomaly Estimation and Layer Potential Techniques

Layer potential techniques have been used widely to deal with the inverse problem of recovering anomalies in a homogeneous background. The reason is that the method provides a concrete expression connecting the anomalies with measured data.

For example, consider the inverse problem of detecting an electrical conductivity anomaly, occupying a region D, inside a three-dimensional region Ω bounded by its surface ∂Ω. Assume that the complex conductivity distribution at angular frequency ω changes abruptly across the boundary ∂D and in . With the aid of the fundamental solution F(r): = − 1/(4π|r|) of the Laplacian, we can provide a rigorous connection between the anomaly D and the boundary voltage–current data via the following integral equation (Kang and Seo 1996): for ,

8.1

where g represents Neumann data corresponding to the sinusoidal injection current with an angular frequency ω, u is the induced time-harmonic voltage inside ...