Numerical Linear Algebra with Applications

16.7 Problems

16.1 Three variables x, y, and z are required to satisfy the equations

$\begin{array}{c}\text{3}x-y+7z=0\\ \text{2}x-y+4z=\text{1}/\text{2}\\ x-y+z=\text{1}\\ \text{6}x-4y+10z=\text{3}\end{array}$

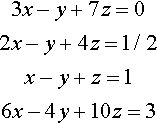
Is there a solution in the normal sense, not a least-squares solution? If so, is it unique, or are there infinitely many solutions?

16.2 If A is an invertible matrix and assuming exact arithmetic, are the solutions using Gaussian elimination and least squares identical? Prove your assertion.

16.3 If A is an m × n matrix, m ≥ n, and b is an m × 1 vector, show that if A^Tb = 0, b is orthogonal to the range of A.

16.4 If A is an m × n full-rank matrix, m ≥ n, show that

$\kappa (A)=||A^{‡}|{|}_{\text{2}}||A|{|}_{\text{2}}=\frac{{\sigma }_{\text{1}}}{{\sigma }_n},$

where σ₁ and σ_n are the largest ...