Numerical Linear Algebra with Applications

Appendix B

Mathematical Induction

This appendix is a brief disussion of the topic, and is intended to be sufficient for the times in the book that a proof uses mathematical induction.

Suppose you are given a statement, S, that depends on a variable n; for instance,

$1+2^2+\dots +n^2=\frac{n\left(n+1\right)\left(2n+1\right)}{6},n\ge 1$

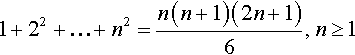
Let n₀ be the first value of n for which S applies, and prove the statement true. This is called the basis step. For our example, n₀ = 1. Now, assume S is true for any n ≥ n₀ and prove that this implies S is true for n + 1. This is called the inductive step.

Then,

• S is true for n₀, so S is true for n₁ = n₀ + 1.

• S is true for n₁, so S is true for n₂ =  ...