October 2013
Beginner to intermediate
576 pages
17h 2m
English
Content preview from Numerical Methods for Engineers and Scientists 3rd Edition
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
Chapter 11
Ordinary Differential Equations: Boundary-Value Problems
Core Topics
The shooting method (11.2).
The finite difference method (11.3).
Use of MATLAB built-in functions for solving boundary value ODEs (11.4)
Complementary Topics
Error and stability in numerical solution of boundary value problems (11.5).
11.1 BACKGROUND
A specific solution of a differential equation can be determined if the constraints of the problem are known. A first-order ODE can be solved if one constraint, the value of the dependent variable (initial value) at one point is known. To solve an nth-order equation, n constraints must be known. The constraints can be the value of the dependent variable (solution) and its derivative(s) at certain values of the independent variable. When all the constraints are specified at one value of the independent variable, the problem is called an initial value problem (IVP). Solution of initial value problems is discussed in Chapter 10. In many cases there is a need to solve differential equations of second and higher order that have constraints specified at different values of the independent variable. These problems are called boundary value problems (BVP), and the constraints are called boundary conditions because the constraints are often specified at the endpoints or boundaries of the domain of the solution.
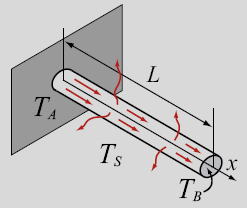
Figure 11-1: Heat flow in a pin fin.
As an example, ...
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.