Optical Communications, 2nd Edition

1.6 FIELD EXPANSIONS

In the analysis of communication systems, it is often convenient to use orthogonal expansions of signals to formulate a more general procedure, and sometimes to gain further insight into results [10]. Orthogonal expansions produce mathematically valid waveform representations that permit signals to be treated in pieces (multiple dimensions) rather than as a single entity. Likewise, in optical communications it is convenient to represent optical fields in terms of similar orthogonal expansions as an alternative to field description.

Consider again a general complex optical field defined over an area A as

where we have denoted a(t, r) as the complex envelope and ω_o as the optical source frequency. Let us now consider a spatial orthogonal expansion of this complex envelope as

where {Φ_i(r)} are a set of complex two-dimensional orthogonal space functions defined over A. That is,

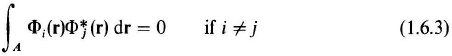
with the asterisk denoting complex conjugates. The corresponding expansions functions are given by

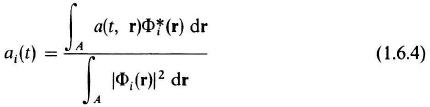
That is, each a_i(t) is the complex time function corresponding to the spatial function Φ_i