Optical Sources, Detectors, and Systems

1.5 Units and Intensity Calculations

21

1.5 Units and Intensity Calculations

We close this chapter by first listing the important numerical

constants that are necessary for our calculations. These are

q electron charge

k Boltzmann's constant

h Planck's constant

c velocity of light

1.6 xW''^^coulombs

138xlO-^^jouleslK

6.6 X10'^^ joule-seconds

3.00 xlO^ meter I second

We also use wavelength and frequency interchangeably and note

that the wavelength X is given by c/v. Figure 1.12 encompasses the

frequencies and wavelengths that are of concern to us, namely that re-

gion from the infrared to the ultraviolet where there is usable atmo-

spheric transmission and where the photon energy hv is much greater

than the thermal energy kT at room temperature.

For convenience in calculations it is often helpful to measure these

energies in electron volts, eV, the energy gained by an electron through

a potential drop of one volt, 1.6 x

10~^^

J. In this measure there are two

simple expressions to remember. These are

10

13

30

jLim

INFRARED

VISIBLE

10

14

"H

3 jj,m

3000 nm

30,000A

ULTRAVIOLET

10

15

±-^ v(Hz)

10

16

0.3 jam

300 nm

3000A

30 nm

300A

Figure 1.12 Infrared, visible, and ultraviolet frequencies and wavelengths.

22 Chapter 1 Blackbody Radiation^ Image Plane Intensity, and Units

hvieV)= hv/q

= hc/qX =

1.24/X(jiim)

kT(eV)

= kT/q - 0.026

(T/300)

Thus,

at room temperature, 300 K, the thermal energy kT is

0.026

eV, while the "photon" energy at a wavelength of 1 jim or 10,000

angstrom units, is 48 times as large or 1.24 eV. This is why there is

effectively zero visible light radiated by room temperature objects.

A final help in performing radiation calculations is an expression for

the fractional amount of radiated power from a blackbody occurring at

wavelengths shorter than a given value X. This may be obtained by

evaluating the expression

K>,).4j-^;

,.^ 0.25)

7t^ J^ (ey - V kT

obtained from Eq. (1.17). Here

I(>x)

has a maximum value of unity and

decreases as the minimum photon energy increases from zero. Since, as

we will learn, most detectors only respond above a given photon energy

(or below a given

"cut-off"

wavelength), the appropriate spectrum-

limited radiance may be obtained by taking the product,

H>x)ecfT'^.

The

emissivity e should of course be an appropriate weighted average.

Since F(x) falls off almost exponentially at high photon energies, a

choice of the emissivity at the cut-off wavelength usually gives an accu-

rate answer. The function

l(>x)

is plotted in Fig. 1.13.

Example: Calculate the power in W/m^ radiated by a unit emis-

sivity surface at temperature 2000 K at wavelengths less than I jUm.

First,

oT^

=

5.67

xl0-^(2000)^

=

9.1

xlO^W/m^.

and we then find x = hv/kT from hv

= (1.24/1)

^ 1.24 eV and kT =

0.026(2000/300) = 0.17 eV The argument, x, becomes 7.3 and

l(>x) =

0.067.

The final radiance is then 6 xW or

60

kW/m^.

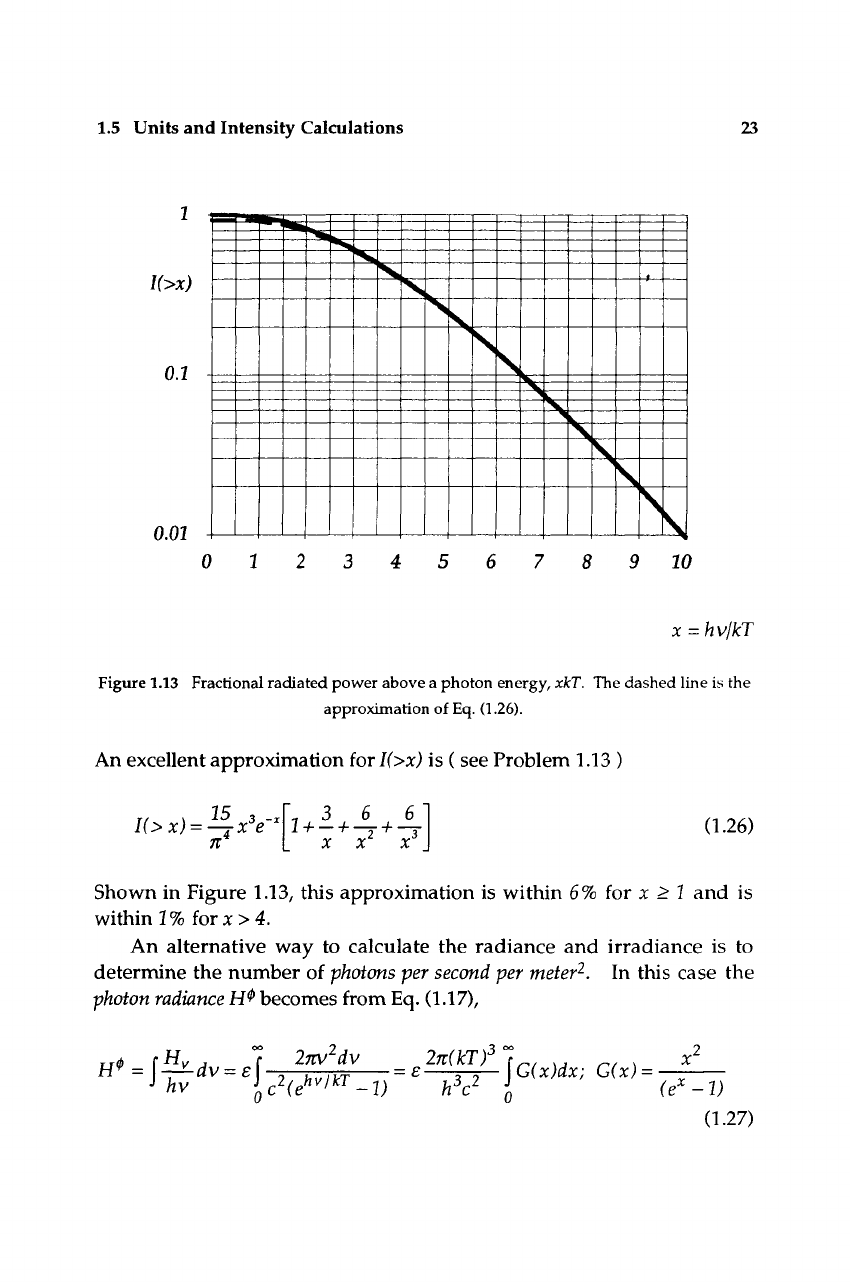
1.5 Units and Intensity Calculations 23

I(>X)

0.1

om

t-

10

X =

hv/kT

Figure 1.13 Fractional radiated power above a photon energy, xkT. The dashed line is the

approximation of

Eq.

(1.26).

An excellent approximation for

I(>x)

is ( see Problem 1.13 )

n

\ 3 6 6'

XXX

(1.26)

Shown in Figure 1.13, this approximation is within 6% for x > I and is

within

17o

for:c>4.

An alternative way to calculate the radiance and irradiance is to

determine the number of

photons

per

second

per

meter^.

In this case the

photon radiance

H^ becomes from Eq. (1.17),

litv^dv

^ = —s^dv = e ^ ,^..rj, =

e—r-^—

G(x)dx;

G(x)--

(e^'-l)

(1.27)