Physically Based Rendering, 3rd Edition

14: Light Transport I: Surface Reflection

This chapter brings together the ray-tracing algorithms, radiometric concepts, and Monte Carlo sampling algorithms of the previous chapters to implement two different integrators that compute scattered radiance from surfaces in the scene. Integrators are so named because they are responsible for evaluating the integral equation that describes the equilibrium distribution of radiance in an environment (the light transport equation).

Recall the scattering equation from Section 5.6.1; its value can be estimated with Monte Carlo:

$\begin{array}{lll}{L}_{\mathrm{o}}\left(\mathrm{p},{\omega }_{\mathrm{o}}\right)\hfill & =\hfill & {\int }_{{\mathcal{S}}^2}f\left(\mathrm{p},{\omega }_{\mathrm{o}},{\omega }_{\mathrm{i}}\right)L_{\mathrm{i}}\left(\mathrm{p},{\omega }_{\mathrm{i}}\right)|cos{\theta }_{\mathrm{i}}|\mathrm{d}{\omega }_{\mathrm{i}}\hfill \\ \approx \hfill & \frac{1}{N}{\displaystyle \sum _{j=1}^N\frac{f\left(\mathrm{p},{\omega }_{\mathrm{o}},{\omega }_j\right)L_{\mathrm{i}}\left(\mathrm{p},{\omega }_j\right)|cos{\theta }_j|}{p\left({\omega }_j\right)}\text{,}}\hfill \end{array}$

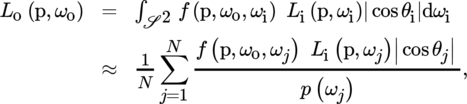
with directions ω_j sampled ...