Chapter 11
Frequency-Domain Filtering
What will we learn?
- Which mathematical tools are used to represent an image's contents in the 2D frequency domain?
- What is the Fourier transform, what are its main properties, and how is it used in the context of frequency-domain filtering?
- How are image processing filters designed and implemented in the frequency domain?
- What are the differences between low-pass and high-pass filters (HPFs)?
- What are the differences among ideal, Butterworth, and Gaussian filters?
11.1 Introduction
This chapter builds upon the ideas introduced in Section 2.4.4, which state that some image processing tasks can be performed by transforming the input images to a different domain, applying selected algorithms in the transform domain, and eventually applying the inverse transformation to the result. In this chapter, we are particularly interested in a special case of operations in the transform domain, which we call frequency-domain filtering. Frequency-domain filters work by following a straightforward sequence of steps (Figure 11.1):
Figure 11.1 Frequency-domain operations.
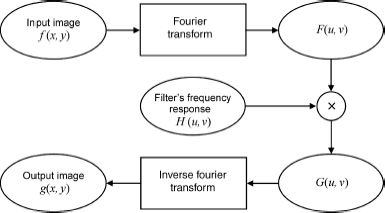
1. The input image is transformed to a 2D frequency-domain representation using the 2D Fourier transform (FT).
2. A filter of specific type (e.g., ideal, Butterworth, Gaussian) and behavior (e.g., low pass, high pass) is specified and applied to the frequency-domain representation of the ...

