Pricing in General Insurance

187

14

Frequency Modelling: Selecting and

Calibrating a Frequency Model

The objective of frequency modelling is the production of a model that gives you the prob-

ability of a given number of losses occurring during a given period, such as the policy

period or a calendar year. As is the case with all models we use for pricing, the frequency

model may be based to a varying extent on past losses, but it is a prospective model, that

is, it tells you what the number of losses will be in the future. As such, loss experience will

have to be adapted to current circumstances before it can be used (Figure 14.1).

Figure 14.2 gives an example of how a frequency model (in this case a Poisson model

with an average frequency of 7) might look like: as an example, it tells us that the probabil-

ity of having exactly four claims is approximately 0.091, and that the probability of having

up to four claims is approximately 0.173.

Theoretically, there are innitely many models that one could use for frequency. In prac-

tice, however, because there are only a small number of years/periods of experience that

one can use to t a frequency model (typically 5–10 years, but it can be as small as 1 year) it

is not possible to discriminate between many models, and in the spirit of statistical learn-

ing (see Section 12.3), it is better to rely on a few well-tested models that one can trust and

that are analytically tractable and choose from among them rather than having a large

dictionary of models that one can choose from on the basis of imsy statistical evidence.

The three most popular models used in insurance are probably the binomial distribution, the

Poisson distribution and the negative binomial distribution. All three of them are so-called ‘count-

ing distributions’, that is, discrete distributions with values over the natural numbers only.

The main practical difference between these three models is that they have different

variance/mean ratios: this is 1 for the Poisson distribution, less than 1 for the binomial

distribution and greater than 1 for the negative binomial distribution. A calculation of the

variance/mean ratio of the number of claims over a certain period may therefore be the

factor that drives the choice of what model is used, although, as we will soon show, things

are more complicated than that.

In practice, the binomial distribution (and its relative, the multinomial distribution) is

normally used with the individual risk model, whereas the Poisson and negative binomial

are used with the collective risk model.

Not only are these three models very simple but they also have some useful properties:

all of them are part of the Panjer class, and they are the only distributions belonging to this

class. The Panjer class (also referred to as the [a,b,0] class) is characterised by the fact that

there exist constants a and b such that

p

p

a

b

k

k

k

k−

=+

=…

1

123

,,

, (14.1)

where p

k

is the probability of having exactly k losses, and p

0

is uniquely determined by

imposing the condition

p

k

k

=

=

∞

∑

1

0

.

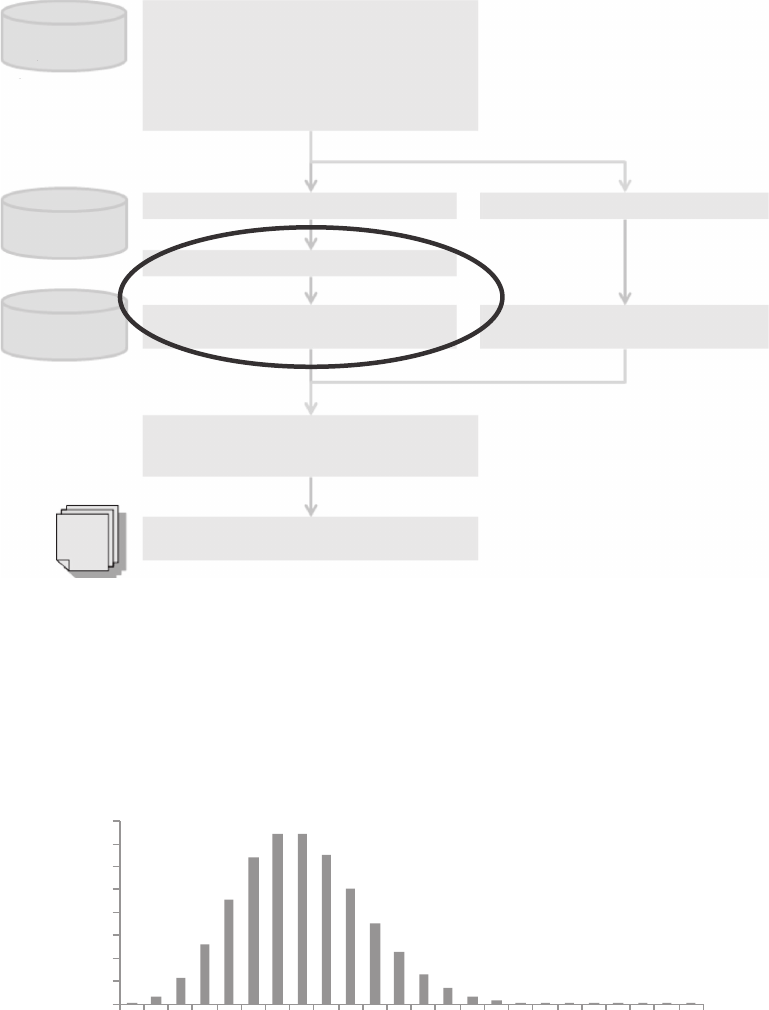
188 Pricing in General Insurance

Individual

loss data

Assumptions on

– Loss inflation

– Cu

rrency conversion

– …

Exposure

data

Portfolio/market

information

Data preparation

– Data checking

– Data cleansing

– Data transformation

– Claims revaluation and currency conversion

– Data summarisation

– Calculation of simple statistics

Inputs to frequency/severity analysis

Adjust historical claim counts for IBNR

Adjust for exposure/profile changes

le

Select frequency distribution and

calibrate parameters

Adjust loss amounts for IBNER

Severity model

Frequency model

Estimate gross aggregate distribution

e.g. Monte Carlo simulation, Fast Fourier

transform, Panjer recursion…

Gross aggregate loss model

Ceded/retained aggregate loss model

Allocate losses between (re)insurer and

(re)insured

Cover

data

Se ct severity distribution and

calibrate parameters

FIGURE 14.1

How selecting and calibrating a frequency model ts in the risk costing subprocess.

0

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

012345678910 11 12 13 14 15 16 17 18 19 20 21 22

No. of claims

Probability

Frequency Model - An Example

Poisson with Rate = 7

FIGURE 14.2

An example of a frequency distribution – a Poisson distribution with rate = 7. The distribution is obviously

asymmetrical – only numbers greater than or equal to 0 have a probability greater than 0, whereas the distribu-

tion extends indenitely to the right.