Probabilistic Design for Optimization and Robustness for Engineers

2 Statistical background for engineering design

This chapter presents a foundation of basic statistics required to understand the concepts covered in later chapters. Topics covered include statistical functions, expectation, statistical distributions, distribution parameters, and sampling.

2.1 Expectation

Probability density functions are grouped into two categories: discrete and continuous. The values a discrete density function can take on are limited to integers. For example, in five flips of a coin, the number of heads is limited to 0, 1, 2, 3, 4, or 5; the value 3.7 is nonsense. Continuous density functions can take on all values in a specific range. For example, the time to fail may be 1 hour, 1.01 hours, 1.001 hours, 1.0001 hours, etc.

To qualify as a density function, two criteria must be met:

1. f(x) ≥ 0

   for all values of x and

2. ∫^∞_{− ∞}f(x)dx = 1

   for continuous distributions, or for discrete distributions,

   

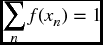
   where the sum is taken over all possible values of n.

The cumulative distribution function is the area under the probability density function to the left of the specified value, and represents the probability of x being less than a specific value, P(X < x). For continuous distributions, the cumulative distribution function is defined as

(2.1)

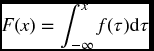
The probability of ...