Probability: An Introduction with Statistical Applications, 2nd Edition

Chapter 2Discrete Random Variables and Probability Distributions

At this point, we have considered discrete sample spaces and we have derived theorems concerning probabilities for any discrete sample space and some of the events within it. Often, however, events are most easily described by performing some operation on the sample points. For example, if two dice are tossed, we might consider the sum showing on the two dice; but when we find the sum, we have operated on the sample point seen. Other operations, as we will see, are commonly encountered.

We want to consider some properties of the sum; we start with the sample space. In this example, a natural sample space shows the result on each die and, if the dice are fair, leads to equally likely sample points. Then, the sample space consists of the 36 points in

These points are shown in Figure 2.1.

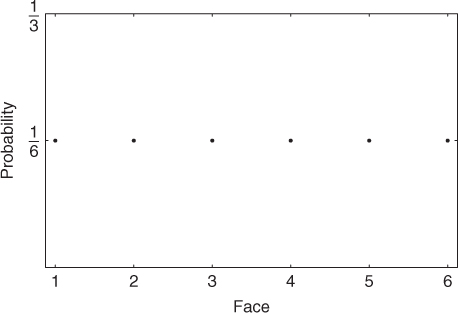
Figure 2.1 Discrete uniform probability distribution.

If we consider the sum on the two dice, then a sample space

might be considered, but now the sample points are not equally likely.

We call the sum in this example a random variable ...