Probability: An Introduction with Statistical Applications, 2nd Edition

Chapter 3Continuous Random Variables and Probability Distributions

3.1 Introduction

Discrete random variables were discussed in Chapter 2. However, it is not always possible to describe all the possible outcomes of an experiment with a finite, or countably infinite, sample space. As an example, consider the wheel shown in Figure 3.1 where the numbers from 0 to 1 have been marked on the outside edge.

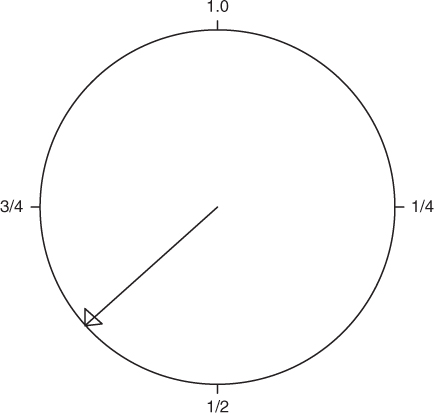
Figure 3.1 The spinner.

The experiment consists of spinning the spinner and recording where the arrow stops. It would be natural here to consider the sample space, , to be

is infinite, but not countably infinite.

Now the question arises, “What probability should be put on each of the points in ?” Surely, if the wheel is fair, each point should receive the same probability and the total probability should be 1. What value should that probability be?

Suppose, for the sake of argument, that a probability of 0.0000000000000000000001 = 10⁻²² is put on each point. It is easy to show that ...