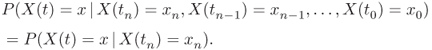Chapter 8Continuous-Time Markov Chains
8.1 Introduction
The analysis of continuous-time Markov chains (CTMCs) is similar to that of the discrete-time case, except that the transitions from a given state to another state can take place at any instant of time. As in the last chapter, we confine our attention to discrete-state processes. This implies that, although the parameter t has a continuous range of values, the set of values of 
is discrete. Let 
denote the state space of the process, and 
be its parameter space. Recalling from Chapter 6, a discrete-state continuous-time stochastic process 
is called a Markov chain if for 
, with t and 
, its conditional pmf satisfies the relation
The behavior of the process is characterized by (1) the initial state probability vector of the CTMC ...
Get Probability and Statistics with Reliability, Queuing, and Computer Science Applications, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
