F.6 CRAMÉR–RAO INEQUALITY
The Cramér–Rao inequality provides a lower bound on the variance of an estimator; it is also called the Cramér-Rao lower bound (CRLB). The CRLB is useful as a performance measure for biased and unbiased estimators of the parameters of a distribution, as described in Chapter 9. We provide a derivation for an unbiased estimator, and state the results for a biased estimator and then for a vector of parameters.
Theorem F.11 (Cramér–Rao inequality). Let T be an unbiased estimator for the function 
of scalar parameter 
where 
are iid samples with pdf 
. Let T = t be a specific value of the estimator for outcomes 
, and assume the following regularity conditions:
- Differentiation with respect to the parameter:
(F.46)
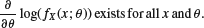
- Differentiation and integration exchange I:
(F.47)
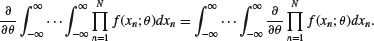
Get Probability, Random Variables, and Random Processes: Theory and Signal Processing Applications now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
