Problems and Solutions in Mathematical Finance: Stochastic Calculus, Volume I

2.2.2 Markov Property

1. 1. The Markov Property of a Standard Wiener Process. Let 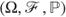be a probability space and let 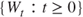be a standard Wiener process with respect to the filtration 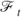, 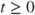. Show that if 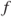is a continuous function then there exists another continuous function 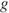such that
   

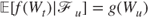
   for .

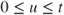   Solution

   For 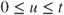we can write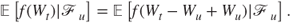

   

   Since 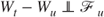and is measurable, by setting where is a constant value

   Because we can write