- 12. Compound Poisson Process. Let
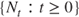be a Poisson process with intensity 
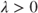defined on the probability space 
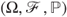with respect to the filtration 
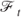, and let 
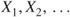be a sequence of independent and identically distributed random variables with common mean 
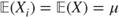and variance 
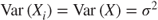. Let 
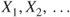be independent of 
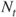. By defining the compound Poisson process 
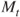as
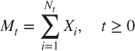
show that the moment generating function for is
where .
Further, show that ...
Get Problems and Solutions in Mathematical Finance: Stochastic Calculus, Volume I now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
