G.2. Relationship between Binary, Octal, and Hexadecimal Numbers
From Table G.1 we see that 3 bits are needed to represent any octal digit, and 4 bits to are needed to represent any hexadecimal digit. We can use this fact to convert between binary, octal, and hexadecimal systems, as shown in Figure G.1.
Figure G.1. Converting between Binary, Octal, and Hexadecimal
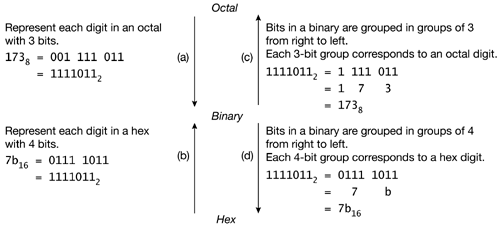
The procedure for converting an octal to a binary is shown by the arrow marked (a). We can prove that replacing each octal digit by its 3-bit equivalent binary value gives the right result:
| 1738 | = 1×82 | + 7×81 | + 3×80 |
| = 1×(23)2 | + 7×(23)1 | + 3×(23)0 | |
| = 1×26 | + 7×23 | + 3 | |
| = (0012)×26 | + (1112)×23 | + (011 ... |
Get Programmer's Guide to Java™ Certification, A: A Comprehensive Primer, Second Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

