Programming Quantum Computers

Chapter 7. QFT: Quantum Fourier Transform

The Quantum Fourier Transform (QFT) is a primitive allowing us to access hidden patterns and information stored inside a QPU register’s relative phases and magnitudes. While amplitude amplification allowed us to turn relative-phase differences into READable differences in magnitudes, we’ll see that the QFT primitive has its own distinct way of manipulating phases. In addition to performing phase manipulation, we’ll also see that the QFT primitive can help us compute in superposition by easily preparing complex superpositions of a register. This chapter begins with some straightforward QFT examples, and then dives into subtler aspects of the tool. For the curious, “Inside the QPU” will examine the QFT operation by operation.

Hidden Patterns

Let’s make our state guessing game from Chapter 6 a little harder. Suppose we have a four-qubit quantum register containing one of the three states (A, B, or C) shown in Figure 7-1, but we don’t know which one.

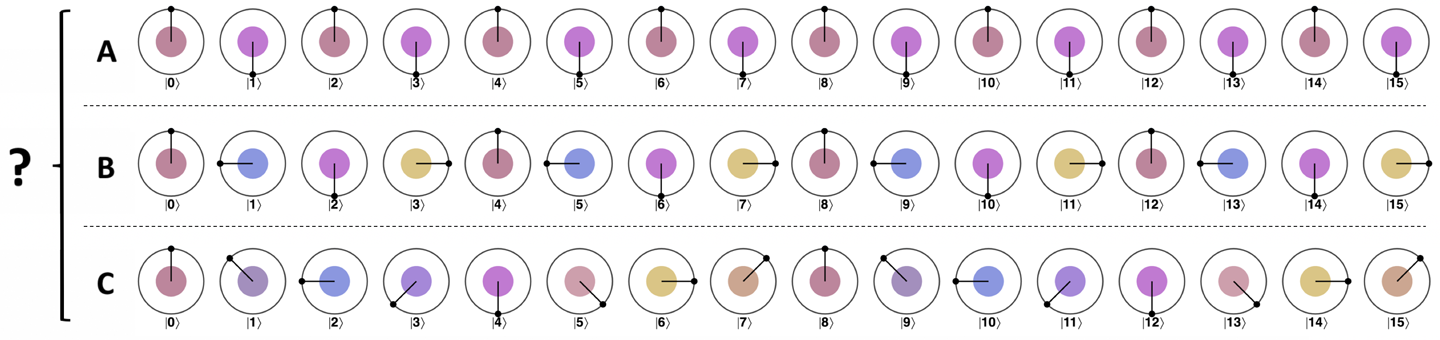
Figure 7-1. Three different states, before applying QFT

Note that these are not the same A, B, and C states that we discussed in the previous chapter.

Visually we can tell that these states are different from each other, but since the magnitudes of all values in each of these states are the same, reading the register returns an evenly distributed random value, regardless of which state it was ...