Propagators in Quantum Chemistry, 2nd Edition

Chapter 3

Propagators and Second Quantization

The Schrödinger equation for an electron or for N noninteracting electrons is

with units such that Planck’s constant is 2π and the electron mass is 1, and with ξ = (, ζ) being a combined space-spin variable. The wave function or Schrödinger amplitude (ξ, t) can be expressed in an orthonormal basis {u_s(ξ)} as

giving the Schrödinger equation in discrete form

The notation

has been employed.

Let x be a unitary transformation to energy eigenstates: x^†x = xx^† = 1, x^†hx = ∊ (diagonal). A formal solution to Eq. (3.3) may be written as

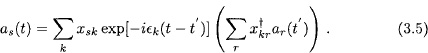
The system may be prepared such that |a_r(t′)|² = 1, and |a_s(t′)|² = 0 for s ≠ r. Then the quantity

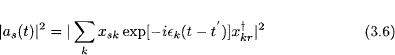
is the probability ...