Quantitative Risk Management: A Practical Guide to Financial Risk, + Website

11.7 Static Models—Threshold and Mixture Frameworks

Threshold and Bernoulli Mixture Models

The static (fixed time period) structural models discussed in Section 11.5 were formulated as threshold models: default (or ratings transition) occurs when a critical variable X crosses below a critical threshold d. Joint default for two firms is determined by the joint probability that both threshold variables are below their respective critical thresholds:

In many cases, the X_i are assumed jointly normal so that this is a statement about a bivariate (or for more than two, multivariate) normal distribution.

When the threshold variables are formulated using the common factor structure of (11.15), the model can alternatively be represented as a Bernoulli mixture model. Bernoulli mixture models have a number of advantages, particularly for simulation and statistical fitting (cf. McNeil, Frey, and Embrechts 2005, section 8.4).

The definition for the common factor structure is equation (11.15), reproduced here.

(11.15)

Conditional on F, the threshold variables X_i are independent because the ε_i are independent. This means the joint default process is independent, conditional on F:

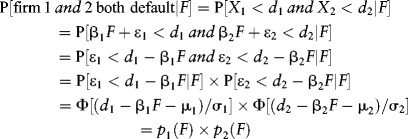
where the final-but-two ...