January 2005
Intermediate to advanced
314 pages
7h 49m
English
Content preview from Quantum Computing and Communications: An Engineering ApproachBecome an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
12
Mathematical Background
Proofs that odd numbers are prime:
- Mathematician: 1 is prime, 3 is prime, 5 is prime, 7 is prime, therefore, by induction, all odd numbers are prime.
- Physicist: 1 is prime, 3 is prime, 5 is prime, 7 is prime, 9 is a bad data point, 11 is prime, 13 is prime…
- Engineer: 1 is prime, 3 is prime, 5 is prime, 7 is prime, 9 is approximately prime, 11 is prime, 13 is prime…
- Computer scientist:1 1 is prime, 1 is prime, 1 is prime, 1 is prime…
12.1 BASIC PROBABILITY THEORY
12.1.1 Characterization of random events
Let A and B denote two random events. If the corresponding probabilities are represented by P(A) and P(B) then we have several important relations:
- OR connection: P (A ∨ B) = P(A) + P(B) − P(A ∧ B). If P(A ∧ B) = 0 then P(A ∨ B) = P(A) + P(B).
- Conditional probability:
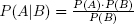. - Independent events: If A and B are independent if and only if P(A ∧ B) = P(A) · P(B) then P(A|B) = P(A).
- Law of total probability:
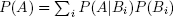. - Bayes formula:
.
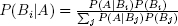A group of mutually excluding probabilistic events {a} belonging to the same observable is represented by means of random variables in probability theory. If variable A stands for a certain random event then the probability of obtaining A = ...
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.