January 2005
Intermediate to advanced
314 pages
7h 49m
English
Content preview from Quantum Computing and Communications: An Engineering ApproachBecome an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
13
Derivations Related to the Generalized Grover Algorithm
13.1 EIGENVALUES OF THE GENERALIZED GROVER OPERATOR
To find the eigenvalues of Q one should solve the characteristic equation det {Q − qI} = 0, which seems to be a fairly hard task
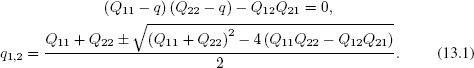
Therefore we follow a more pragmatic way. Applying the basis-independent product of eigenvalues in the form of det {Q} = q1q2 as well as exploiting the form of eigenvalues of unitary operators ejε,
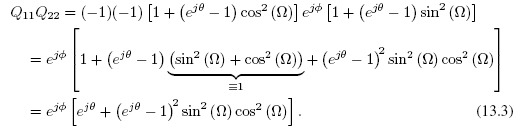
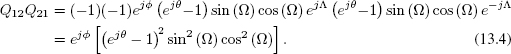
Substituting (13.3) and (13.4) into (13.2) we get
since qi = ejεi, hence the eigenvalues of the generalized Grover operator become
Furthermore, it is known that the trace of Q can be expressed as
resulting in
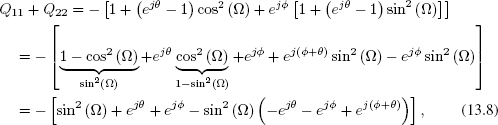
where the equality stands if both the real and ...
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.