Quantum Computing and Communications: An Engineering Approach

Solutions of Exercises

Exercise 2.1: Prove in several different ways that HH = I.

Solution: First we use matrix algebraic multiplication

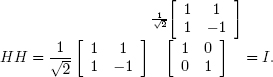
Next we utilize the superposition principle which claims that performing a linear operator on a superposition is equivalent to computing the outcomes with each individual computational basis state as an input and than adding the results together. Since HH|0〉 = |0〉 and HH|1〉 = |1〉 therefore two consecutive Hadamard gates act as an identity transform on their arbitrary superpositions.

Finally we remember that Hadamard gates are Hermitian (H^† = H) and unitary (H^† = H⁻¹) thus HH = HH^† = HH⁻¹ = I.

Exercise 2.2: Prove that HXH = Z, HYH = −Y and HZH = X.

Solution:

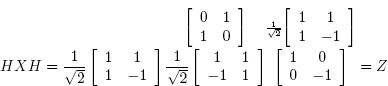
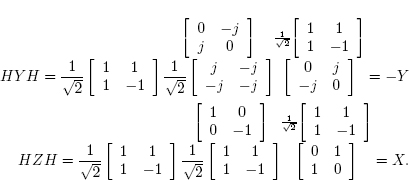
Exercise 2.3: Perform the analysis of the generalized interferometer using the superposition principle.

Solution: We start from |0〉 according to Fig. 2.7. The first Hadamard gate produces

The phase shifter introduces delays independently along the two paths

Finally we apply the second Hadamard ...