Quantum Computing Explained

15

CLUSTER STATE QUANTUM COMPUTING

Cluster state quantum computing is a model that does not rely on quantum gates to do its processing. This measurement based model can instead simulate the unitary dynamics of quantum mechanics. Since quantum gates are implemented using unitary operators, quantum computation can be simulated or implemented using the cluster state model.

A cluster state is a multiple-qubit state that is processed by a series of measurements. Each time a measurement is made, the result of the measurement is used to select the basis used for the next measurement—so this type of quantum computation involves a feedback loop. Cluster state quantum computing can be summarized in two steps:

•   Initialize a set of qubits in some state. For example, start with | + 〉 and then apply controlled phase gates to the states.

•   Measure the qubits in some basis. As the measurement process is repeated, the choice of basis each time is determined by the previous measurement results, creating a feedback process.

A controlled phase operation is the controlled-Z gate with matrix representation in the computational basis

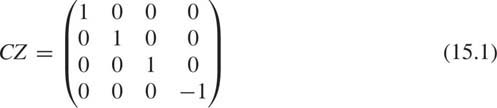
The effect of applying the controlled phase gate is to entangle the states.

CLUSTER STATES

Cluster states are represented by graphs, which are a set of nodes or vertices and edges. Each vertex is a qubit, while the edges represent controlled phase gates. An example is ...