Random Data: Analysis and Measurement Procedures, Fourth Edition

APPENDIX B

Definitions for Random Data Analysis

Autocorrelation Function

The autocorrelation function R_xx(τ) of a quantity x(t) is the average of the product of the quantity at time t with the quantity at time (t + τ) for an appropriate averaging time T:

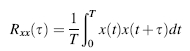
The delay τ can be either positive or negative. For an ergodic process, T should approach infinity, but, in practice, T must be finite. The total mean square value can be estimated by

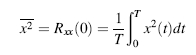
Autospectral Density Function

By finite Fourier transform techniques, the autospectral (also called power spectral) density function G_xx(f) is defined for 0<f<1 by

where E[] is an ensemble average, for fixed f, over n_d available sample records of |X(f, T)|². The quantity X(f, T) is a finite Fourier transform of x(t) of length T. The quantity G_xx(f) = 0 for f < 0.

For theoretical studies, a two-sided autospectral density function S_xx(f) can be defined for − ∞ < f < ∞ by setting

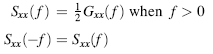
For stationary random data, the autospectral density function G_xx(f) is twice ...