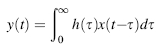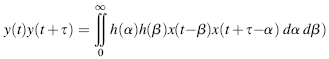CHAPTER 6
Single-Input/Output Relationships
This chapter is concerned with the theory and applications of input/output relationships for single-input problems. It is assumed that records are from stationary random processes with zero mean values and that systems are constant-parameter linear systems. Single-input/single-output (SI/SO) models and single-input/multiple-output (SI/MO) models are discussed. Ordinary coherence functions and optimum frequency response functions are defined for these models. Multiple-input problems are covered in Chapter 7.
6.1 SINGLE-INPUT/SINGLE-OUTPUT MODELS
Consider a constant-parameter linear system with a weighting function h(τ) and frequency response function H(f) as defined and discussed in Chapter 2. Assume the system is subjected to a well-defined single input x(t) from a stationary random process {x(t}} and produces a well-defined output y(t), as illustrated in Figure 6.1. This output will belong to a stationary random process {y(t)}.
6.1.1 Correlation and Spectral Relations
Under ideal conditions, the output y(t) for the system in Figure 6.1 is given by the convolution integral
where h(τ) = 0 for τ < 0 when the system is physically realizable. The product y(t)y(t + τ) is given by
Figure 6.1 Ideal single-input/single-output linear ...