Reliability Engineering

3Probability and Life Distributions for Reliability Analysis

In reliability engineering, data are often collected from analysis of incoming parts and materials, tests during and after manufacturing, fielded products, and warranty returns. If the collected data can be modeled, then properties of the model can be used to make decisions for product design, manufacture, reliability assessment, and logistics support (e.g., maintainability and operational availability).

In this chapter, discrete and continuous probability models (distributions) are introduced, along with their key properties. Two discrete distributions (binomial and Poisson) and five continuous distributions (exponential, normal, lognormal, Weibull, and gamma) that are commonly used in reliability modeling and hazard rate assessments are presented.

3.1 Discrete Distributions

A discrete random variable is a random variable with a finite (or countably infinite) set of values. If a discrete random variable (X) has a set of discrete possible values (x₁, x₂, … x_n), a probability mass function (pmf), f(x_i) , is a function such that

(3.1)

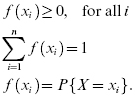
The cumulative distribution function (cdf) is written as:

(3.2)

The mean, μ, and variance, σ², of a discrete random variable are defined using the pmf as (see also Chapter 2):

(3.3)