APPENDIX F Valuing American Options
To value American-style options, we divide the life of the option into n time steps of length Δt. Suppose that the asset price at the beginning of a step is S. At the end of the time step it moves up to Su with probability p and down to Sd with probability 1 − p. For an investment asset that provides no income the values of u, d and p are given by
with
where r is the risk-free rate and σ is the volatility.
Figure F.1 shows the tree constructed for valuing a five-month American put option on a non-dividend-paying stock where the initial stock price is 50, the strike price is 50, the risk-free rate is 10%, and the volatility is 40%. In this case, there are five steps so that Δt = 0.08333, u = 1.1224, d = 0.8909, a = 1.0084, and p = 0.5073. The upper number at each node is the stock price and the lower number is the value of the option.
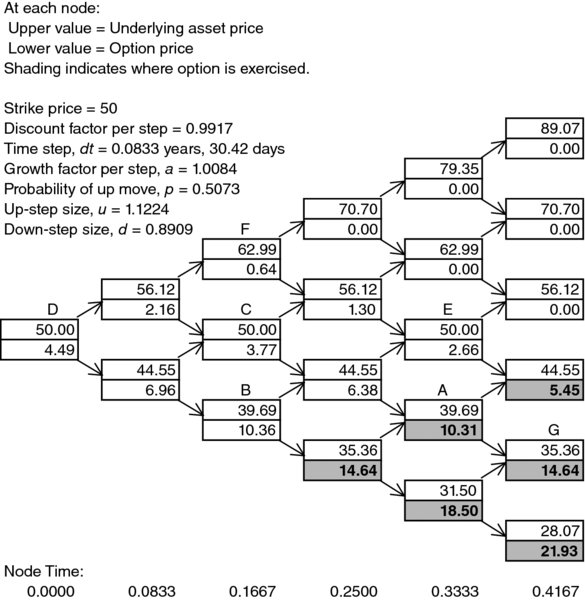
FIGURE F.1 Binomial Tree from DerivaGem for American Put on Non-Dividend-Paying Stock
At the final nodes of the tree, the option price is its intrinsic value. For example, at node G, the option price is 50 − 35.36 = 14.64. At earlier nodes, we first calculate a value assuming that the option is held for ...
Get Risk Management and Financial Institutions, 4th Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

