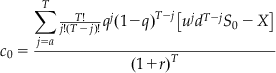Risk Neutral Pricing and Financial Mathematics: A Primer

(5.20)

or:

$\begin{array}{cc}{c}_0& =S_0\left[{\displaystyle \sum }_{j=a}^T\frac{T!}{j!(T-j)!}{q}^j{(1-q)}^{T-j}\frac{u^j{d}^{T-j}}{{(1+r)}^T}\right]-\frac{X}{{(1+r)}^T}\left[{\displaystyle \sum }_{j=a}^T\frac{T!}{j!(T-j)!}{q}^j{(1-q)}^{T-j}\right]\end{array}$

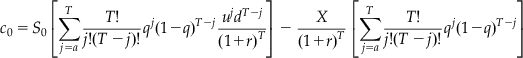
or, in shorthand form:¹²

$c_0=S_{0}B\left[T,q\prime \right]-X{(1+r)}^{-T}B[T,q]$

where q′=qu/(1+r) and 1−q′=d(1−q)/(1+r). The values q′, q, and T are the parameters for the two binomial distributions. Three points are worth further discussion regarding this simplified binomial model:

1. First, as T approaches infinity, the binomial distribution will approach the normal distribution, ...