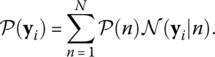Robot Learning by Visual Observation

4Task Modeling

The core programming‐by‐demonstration (PbD) methods for task modeling at a trajectory level of task abstraction are presented in this chapter. The emphasis is on the statistical methods for modeling demonstrated expert actions. The theoretical background behind the following approaches is described: Gaussian mixture model (GMM), hidden Markov model (HMM), conditional random fields (CRFs), and dynamic motion primitives (DMPs). A shared underlying concept is that the intent of the demonstrator in performing a task is modeled with a set of latent states, which are inferred from the observed states of the task, that is, the recorded demonstrated trajectories. By utilizing the set of training examples from the step of task perception, the relations between the latent and observed states, as well as the evolution of the states of the model, are derived within a probabilistic framework.

4.1 Gaussian Mixture Model (GMM)

GMM is a parametric probabilistic model for encoding data with a mixture of a finite number of Gaussian probability density functions. For a dataset Y consisting of multidimensional data vectors y_i, the GMM represented with a mixture of N Gaussian components is (Calinon, 2009)

(4.1)

In (4.1), , for , are the mixture weights for the Gaussian components, calculated ...