Chapter 1 Vector Spaces
1.1 Vector Spaces
The definition of a vector space over a field and that of a subspace of a vector space are given in Section B.6. Our focus in this book is exclusively on vector spaces over the real numbers (as opposed to the complex numbers or some other field).
Throughout, all vector spaces are over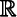 
, the field of real numbers
For brevity, we will drop the reference to ℝ whenever possible and write, for example, “linear” instead of “ℝ‐linear”.
Of particular importance is the vector space ℝ m , but many other examples of vector spaces will be encountered. It is easily shown that the intersection of any collection of subspaces of a vector space is itself a subspace. The zero vector of a vector space is denoted by 0, and the zero subspace of a vector space by {0}. The zero vector space, also denoted by {0}, is the vector space consisting only of the zero vector. We will generally avoid explicit consideration of the zero vector space. Most of the results on vector spaces either apply directly to the zero vector space or can be made applicable with a minor reworking of definitions and proofs. The details are usually left to the reader.
Get Semi-Riemannian Geometry now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
