Semi-Riemannian Geometry

Chapter 22 Applications to Physics

22.1 Linear Isometries on Lorentz Vector Spaces

Let (V, g, D) be an oriented Lorentz vector space, and let ε = (e ₁, …, e _m ) be an orthonormal basis for V that is positively oriented with respect to D. We denote by L _m the set of linear isometries on V:

where we recall that Lin(V, V) is the vector space of linear maps from V to V.

Theorem Theorem 22.1.1 Theorem 22.1.1

L _m is a group (under composition of linear maps), called the Lorentz group on V .

Proof

Let A be a map in L _m . It follows from Theorem 1.1.9 and Theorem 4.4.1(a) that the inverse A ^–1 exists and is in Lin(V, V). Let v, w be vectors in V. Then

so A ¹ is in L _m . The rest of the verification that L _m is a group is straightforward.

Let A be a map in Lin(V, V). For brevity, we denote by , and likewise omit &ip.eop; from the notation for other matrices. Corresponding to (4.4.1) and (4.4.2), we have

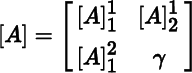
and

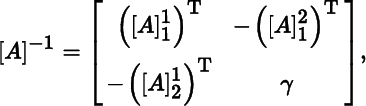
respectively, where

and