Signal Processing for Cognitive Radios

4.4 NONPARAMETRIC SIGNAL DETECTION THEORY

Let us revisit the binary hypothesis testing problem:

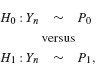
where Y_n, for n = 1,...,N, are assumed to be iid. The parametric signal detection theory considered in the previous section assumed that the observation distributions, P₀ and P₁ (or equivalently the corresponding pdf’s), under the two hypotheses H₀ and H₁, respectively, are completely known, except for a finite number of possibly unknown parameters. Recall that, even in the case of composite hypothesis testing problems in which under each hypothesis the observations can take a set of possible distributions depending on the value of the parameter θ, the set of distributions under each hypothesis are completely parameterized by θ:

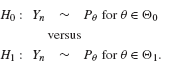
In other words, the theory we have presented in the previous section applies only if the distributions of data under the two hypotheses can be parameterized by a finite set of parameters. Or, we may say, by a finite-dimensional parameter vector.

However, there are practical situations in which the probability density of the observations may not be parameterized by a finite number of parameters under one, or both, of the hypotheses. Usually, this happens due to unknown noise distributions. For example, in sonar problems, it is common to assume that the noise distribution ...