SHORT QUESTIONS AND ANSWERS
Q1. Define the convolution of x(t) with h(t).
Ans.: The convolution of x(t) with h(t) is defined by
Hence the output y(t) is the convolution of h(t) and x(t).
∴ (y) = Convolution of h(t) and x(t) =x(t) * h(t) = 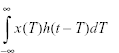
The symbol ‘*’ in Eq. (7.2) stands for convolution.
Q2. State the properties of linear convolution.
Ans.: The linear convolution possesses the following properties:
Commutative property: x1(T)*x2(t) = x2(t)*x1(t)
Associative property: x1(t)*[x2(t) *x3(t)] = [x1(t)*x2(t)] *x3(t)
Get Signals and Systems now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

