Six Sigma Case Studies with Minitab®

200 Six Sigma Case Studies with Minitab

®

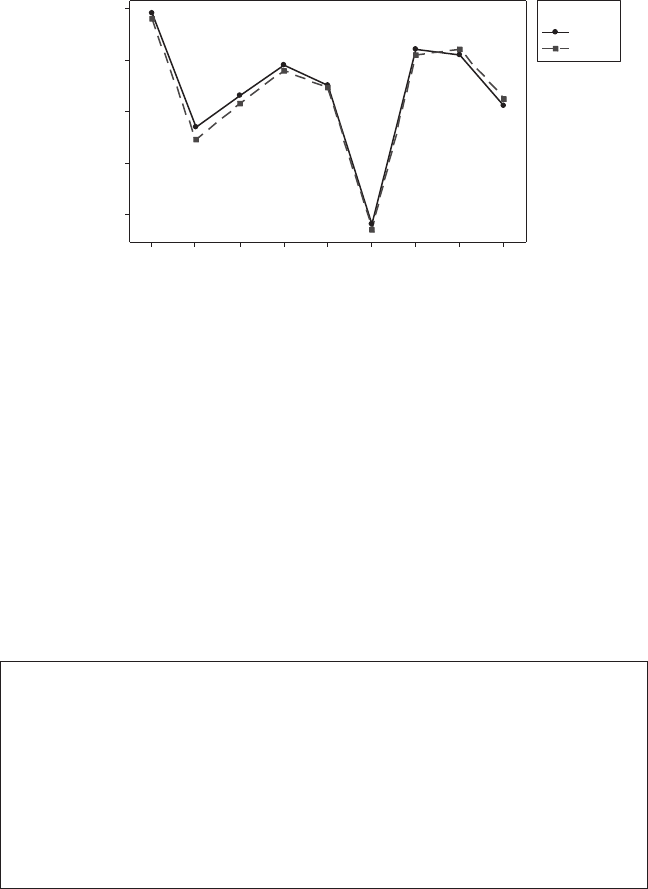
The graph in Figure12.8 shows the

X

___

values of the two operators. The

averages of the

X

___

values are joined with straight lines. Notice that, for each

part, the

X

___

values of the two operators are very close. Hence, this graph

also means that the reproducibility of the measurement system is good. The

graph in Figure12.9 too shows that the average diameters of all the parts for

the two operators are almost equal. (Notice that the line joining the averages

of the two operators is almost horizontal.) Hence, this graph too shows that

the reproducibility of the measurement system is good.

The graph in Figure12.10 is essentially an overlap of the

X

___

charts (shown in

Figure12.7) of the two operators. Because the charts are almost parallel, it means

that there is no signicant interaction between the parts and the operators.

Figures12.11 and 12.12 are excerpts from the session output. Inasmuch as

the default value for “alpha to remove interaction term” in the dialog box

shown in Figure12.5 is 0.25 and the P-value for part and operator interaction

in Figure12.11 is 0.649 (>0.25), Minitab

®

has repeated an ANOVA without the

interaction term (see Figure12.12).

In Figure 12.12, the P-value for Part is 0.00 (<0.05), and the P-value for

Operator is 0.153 (>0.05). It is evident from this output that the variation in

the diameters is due to the differences among parts and not due to variation

between operators.

Figures 12.13 and 12.14 are also excerpts from the session output. It is

clear from the “%Contribution” values (variance values) in Figure 12.13

that just 1.39% of the variation in the diameters is due to variation in gage

987654321987654321

0.0006

0.0004

0.0002

0.0000

Part

Sample Range

R = 0.0001444

UCL = 0.0004719

LCL = 0

12

987654321987654321

9.014

9.012

9.010

Part

Sample Mean

12

UCL = 9.012627

X = 9.012356

LCL = 9.012084

Gage name:

Da

te of study:

XYZ Calipers

03/19/2012

Reported by: John Doe

Tolerance:

Misc:

R Chart by Operator

Xbar Chart by Operator

ABC Project

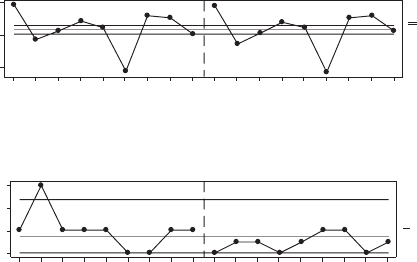
FIGURE 12.7

Xbar and R charts.

201Measurement System Analysis at a Medical Equipment Manufacturer

987654321

9.014

9.013

9.012

9.011

9.010

9.009

Part

Gage name:

Da

te of study:

XYZ Calipers

03/19/2012

Reported by: John Doe

Tolerance:

Misc:

Diameter by Part

ABC Project

FIGURE 12.8

Diameter by part.

21

9.014

9.013

9.012

9.011

9.010

9.009

Operator

Gage name:

Da

te of study:

XYZ Calipers

03/19/2012

Reported by: John Doe

Tolerance:

Misc:

Diameter by Operator

ABC Project

FIGURE 12.9

Diameter by operator.

202 Six Sigma Case Studies with Minitab

®

repeatability and gage reproducibility. Note that 1.30% for repeatability and

0.08% for reproducibility are not adding up to 1.39% due to rounding. Whereas

“% Contribution” in Figure12.13 measures contribution to variance of the data,

“% Study Var” in Figure12.14 measures contribution to standard deviation of

the data.

Notice that none of the graphs in Figures12.6–12.10 shows the individual

part diameters for each trial for each operator. A gage run chart can be used

to show those data. Figure12.15 shows how to plot a gage run chart. Doing so

opens the dialog box shown in Figure12.16. As shown in Figure12.16, select

“Part” for “Part Numbers”, “Operator” for “Operators”, and “Diameter” for

987654321

9.014

9.013

9.012

9.011

9.010

Part

Average

1

2

Operator

Gage name:

Da

te of study:

XYZ Calipers

03/19/2012

Reported by: John Doe

Tolerance:

Misc:

Part* Operator Interaction

ABC Project

FIGURE 12.10

Interaction between part and operator.

Two-Way ANOVA Table with Interaction

Source DF SS MS F P

Part 8 0.0000448 0.0000056 373.407 0.000

Operator 1 0.0000000 0.0000000 2.667 0.141

Part * Operator 8 0.0000001 0.0000000 0.750 0.649

Repeatability 18 0.0000004 0.0000000

Total 35 0.0000453

Alpha to remove interaction term = 0.25

FIGURE 12.11

ANOVA with interaction.

203Measurement System Analysis at a Medical Equipment Manufacturer

“Measurement Data”. Click on the “Gage Info” button, and the dialog box

shown in Figure12.17 opens. Enter the information as shown in Figure12.17

and click on “OK”. It takes you back to the dialog box shown in Figure12.16.

Click on the “Options” button and the dialog box shown in Figure 12.18

opens. Enter the title as shown in Figure12.18 and click on “OK”. It takes you

back to the dialog box shown in Figure12.16. Click on “OK” and the gage run

chart shown in Figure12.19 results. It is clear from the gage run chart that the

repeatability of each operator is good and also the reproducibility between

the two operators is good.

StudyVar %StudyVar

Source StdDev (SD) (6*SD) (%SV)

Total Gage R&R 0.0001402 0.0008412 11.79

Repeatability 0.0001359 0.0008152 11.42

Reproducibility 0.0000346 0.0002075 2.91

Operator 0.0000346 0.0002075 2.91

Part-To-Part 0.0011814 0.0070883 99.30

Total Variation 0.0011897 0.0071380 100.00

FIGURE 12.14

Distribution of standard deviations.

Two-Way ANOVA Table without Interaction

Source DF SS MS F P

Part 8 0.0000448 0.0000056 303.394 0.000

Operator 1 0.0000000 0.0000000 2.167 0.153

Repeatability 26 0.0000005 0.0000000

Total 35 0.0000453

FIGURE 12.12

ANOVA without interaction.

%Contribution

Source VarComp (of VarComp)

Total Gage R&R 0.0000000 1.39

Repeatability 0.0000000 1.30

Reproducibility 0.0000000 0.08

Operator 0.0000000 0.08

Part-To-Part 0.0000014 98.61

Total Variation 0.0000014 100.00

FIGURE 12.13

Distribution of variances.